A. Lehr
Contemporary Dutch Bell-Founding Art
This paper, published in translation in Rossing's book Acoustics of Bells is of interest for a number of reasons. Most importantly, it explains the physical processes involved in bell tuning and in particular where on the inside of the bell the tuner removes metal to tune particular partials. This information is derived from actual measurements on bells. Lehr proposes a partial classification scheme (rather less robust than that of Perrin and Charnley) and goes some way towards explaining how partials other than the 'Simpson' partials matter to the timbre of a bell. He also supplies some information on the amplitude of partials. The historical introduction gives insight into the importance of profile development to improvements in bell sound.
This article was translated by R. Selman and T. Marton from "Hedendaagse Nederlandse Klokkengietkunst," in Neth. Acoust. Soc. Publ. No.7, 1965, pp. 20-49. The text of the paper is reproduced in its entirety. Unfortunately the quality of the diagrams (scans of photocopies) leaves a little to be desired.
HISTORICAL ORIENTATION1
The bell, a very primitive, strongly symbolistic, percussion instrument, originated probably in the second millenium before Christ in the steppe region of central Asia. Excavations as well as drawings have shown that the dimensions of such bells were very small (10 cm diameter); moreover, their sound was highly nonmusical.
Naturally, our concept of a bell of that time, if it really merits the name bell, is not very clear. On the other hand, using our present-day values, we can show very clearly what a stark contrast there is between this primitive beginning and a contemporary west European bell. The latter is melodious and can well serve a musical function. However, before the bell reached this stage, which happened for the first time in seventeenth century Netherlands, there had been a long and laborious development.
Without any clear proof, most publications on bells put the origin of the west European bell in ancient China.2 This is done presumably because the bronze culture, the first condition for founding a bell, was developed in China long before Christ. Moreover, a series of bells have been found from that time that were based on the Chinese scale and must have served as a tuning standard for other musical instruments.
Nevertheless, there are several reasons to doubt that the art of bell founding was introduced into Europe from China. Not only is the Chinese bell with its cylindrical shape of a totally different profile than the oldest European bell, but also in Europe a different and better bronze alloy had been used from the beginning. Above all, the development of the European founding art started from a very primitive stage, which makes any comparison with the highly refined bell art of China at the same time seem rather imaginary.
More plausible seems to be the hypothesis that bell art in the second millenium B.C. spread from the central Asiatic steppes both east to China and to the south. Equestrian tribes from the north also played a decisive role in penetrating into the near East. Even later, the Celts, during their migrations west, did the same thing when they provided their horses and chariots with small bells, which had the function of frightening unfavorable gods during battle. This seems to be the origin of the peaceful cowbells of the Swiss Alps.
The question is, were the conditions in ancient China before Christ really much more favorable for a rich bell art? Probably they were. We cannot rely on the fact that the Chinese possessed the undoubtedly highly developed bronze founding technique that found its expression in innumerable ritual vases. If the bell also found its place in this rich bronze culture, there had to be other factors present as well. We find these present in the curious fact that, in the entire Orient, musical instruments were much more varied than in the countries around the Mediterranean Sea.
The Far East was, and still is, that part of the world where idiophonic instruments are of prime importance. We only have to think of the gamelan, which is also known in The Netherlands, for support of this hypothesis.3 It is therefore not surprising that at an early stage in China, bells were jointed together in series for the purpose of sounding melodies. We can continue this line further by observing that all idiophonic instruments, whether the iron or brass rod of a metallophone, or a brass gong; or even a bell, without special precautions will contain non-harmonic overtones and will thus be unsuitable for music that has a definite structure, that is, polyphony. Is this the reason why in the Far East music has remained primarily melodic? Do we have to assume that the earliest musicians there unconsciously understood the impossibility of sounding instruments together harmonically which themselves had no harmonic structure? This all seems more plausible if we also consider the contrast with West European music, which came to be as we understand from the Near East. For there, even if one deviated from the human voice with its harmonic structure, one chose predominantly stringed instruments that also possessed harmonic overtones.
Making a big jump in time, to the end of the Middle Ages, when polyphony started to clearly form and instrumental music obtained an independent value, primarily harmonic instruments still determined the musical culture. On a theoretical level, the discussion of the division of the octave into 12 tones demonstrates this situation very clearly.4 The great problem was the question of how one could make this division without creating too many disturbing deviations from the harmonic series. If strings and organ pipes were not mutually tuned harmonically, it would be necessary to minimize the expected beats for polyphonic consonance. The tuning principle that remained valid for the longest time, until the eighteenth century, was the so-called mean-tone tuning, in which one minimized the beats in the most usual chords. The consequence was an imaginary fifth g#-eb in which the beats were intolerable and resembled the howling of wolves, thus the wolf-fifth.
From this contrast between the polyphonic music of west Europe with harmonic overtones and the homophonic Chinese music with nonharmonic overtones, one can expect that if anyone were to develop a harmonic bell or carillon, it should have been done in Europe. For it is clear that a carillon of bells without harmonic overtones does not properly belong in Europe, at least if one were to try playing polyphonic music on bells, or with other instruments.
In contrast with the single pealing bell, in which one could accept the nonharmonic overtone structure, is the carillon where one is faced with the disagreeable consequences of a nonharmonic overtone structure. It is not incidental that this problem became more and more urgent as polyphony developed.
From all of this one can get the impression that the problem of tuning bells was especially one of internal tone structure. There were additional complications, however, in that one also had to tune the strike note of one bell to another, much more complicated than the mutual tuning of the strings of a piano or the pipes of an organ, although the problems are similar. This problem of tuning the internal harmonic structure for each bell (the ratios of the eigenfrequencies) as well as external tuning from bell to bell (the correct ratio between the principal tones) was already felt in the sixteenth century but only resolved in the seventeenth century. As a chronicle writer of the sixteenth century has indicated, the carillon is typically a development of the Low Countries, where one is impressed by the beauty and wealth of the churches and by the size and beautiful sound of the bells, on which one can play songs as on guitars.
Can one discern a clear evolution starting with the steppe region of Central Asia a thousand years before Christ to the end of the Middle Ages in the Low Countries? Not at all. For in spite of the fact that all civilizations around the Mediterranean have had small bells since antiquity, the bells never emerged beyond the beginning stage, and their function in daily life was limited to simple signal instruments or the clearly sacred function of frightening demons. Any significance of the bell as a musical instrument was absent. Illustrating this is, for example, the Old Testament story about the high priest who enters the holy of holies. The prescripts required that little bells should hang from the border of his robe, not to enhance the spectacle of his entrance, but to frighten evil so that he could enter in a state of purification.
If we really want to look for the true origin of present-day bell art, we only have to go back a thousand years in history to the time when missionaries from Anglo-Saxon countries brought in bells of Celtic origin. Not long after, ca. 1000 A.D., cymbal playing originated in several Benedictine monasteries; it is the most ancient precursor of the present-day carillon. Eight or more little bells tuned to the diatonic scale were joined together. These were used for musical instruction, clockworks of later dates, and as an additional organ register.5
The method used by the Medieval monks to design this tone sequence was mathematically beautiful but fundamentally incorrect. They reasoned, for example, that an octave interval between two bells (frequency ratio of 2:1) could be realized by having the weights of the bells also in the ratio of 2:1; this meant that the octave bell was to be roughly twice as thick.6 One can take the frequency to be linearly proportional to wall thickness. This rule, by Rayleigh, is only valid for hypothetically thin-walled shells.7 In practice one really cannot obtain a frequency doubling, but less than that, so that the octave bell must have been considerably low. But perhaps we should be thankful that the Medieval people applied this simple theory because, completely in accord with the spirit of that time, they did not dare doubt their arithmetic rule, but suspected that the deviations were caused by mistakes in the founding. This was a reason for them to start tuning the little bells. Thus the origin of bell tuning. One may have noticed the cymbals were considered only as far as their external tuning and that one only paid attention to the mutual tuning of the little bells. There was no objection to this, because one can assume that these cymbals only produced simple homophonic music. Nevertheless, even if one had some idea of the frequency ratios of overtones, one would have been in an even more hopeless situation. For the discovery that internal tone structure is highly dependent on the profile came much later. The profile, however strange this may seem, was not controlled until very late in the Middle Ages.
During the entire Middle Ages, until the beginning of the fourteenth century, the bell was not formed with the help of a template, but was almost entirely made free hand .8 Only a few main dimensions had been fixed a priori. Particularly uncertain were the various curves in the bell model that are so important for internal tuning. A systematic profile investigation had never been made, because two bell models were never the same. In fact, the bell founder of that time was mainly impressed with relating the main dimensions of various bells by simple ratios. It is clear that this cannot have any significance for the sound of any particular bell.
However, from the beginning of the fourteenth century, templates were used in bell founding, and we see some great changes in bell science. This happened in particular at the end of the fourteenth century when the principle of dynamic similarity was discovered experimentally. This principle states that corresponding eigenfrequencies with corresponding nodes, cast in the same bronze with the same structure, are inversely proportional to the dimensions. An octave bell could therefore be realized by having all dimensions a factor of two smaller. Nevertheless, this does not mean that from that time the strike tones of bells were correct relative to each other. For in spite of the fact that the profile could be designed very accurately, and one could scale the profiles using pythagorean numbers, even to this day uncertain factors during forming and casting make the cast bell something different than what was designed on paper. The consequence was that correction of the bell profile after forming remained necessary, and one therefore had to tune the bell. Since the middle of the sixteenth century this has been done with most carillons.
Adoption of the template meant that the fundamental conditions for determining the relationship between bell profile and overtone structure had been found. One could now cast various profiles and try to relate these to the variation of the relationship between the overtones of a bell. Without a template this would have been impossible.
The introduction of the template was not the final development because one also had to measure the frequencies. This was only done a couple of centuries later. The development of the measuring technique is due to the famous seventeenth century bell founders, brothers Francois and Pieter Hemony.9 Our conclusion is that, since the end of the Middle Ages until the beginning of the seventeenth century, attempts to give bells internal harmonic structure were more directed than earlier times but were never successful because they lacked a good measurement technique for the overtones. This will be discussed in the next section.
FREQUENCY MEASUREMENTS IN BELL FOUNDING
Once the bell was accepted as a musical instrument in western Europe at the end of the Middle Ages, an appropriate method for measuring the sound of a bell was sought. Of course the oldest method was to compare the pitch with that of another musical instrument such as the organ. In the sixteenth century one finds that occasionally the bell founder was sent an organ pipe with the request to make a bell that had the same pitch.10 Clearly this method could be successful only for external tuning; one could only compare the general impression of the bell tone with that of the organ pipe. Adequate bell tuning at that time meant that one tried thinning the wall to make the impression of the bell sound the same as the organ pipe. Really fruitful bell-sound analysis could begin only by analysing the sound of the bell. This only would make it possible to draw conclusions about the internal structure of the bell sound and relate this to the bell profile.
The impulse to do this was given by the impossibility of playing polyphonic harmonized music on bells. Jacob van Eijck, famous musician and carilloneur in the beginning of the seventeenth century, pointed this out repeatedly, particularly to Bacon, Descartes, and Mersenne. Certainly Van Eijck's greatest accomplishment is that he developed a method for measuring the bell partials individually. He would demonstrate the method, by whistling at the pitch of one of the eigenfrequencies of wine glasses, so that the wine glass would start resonating. This instructive experiment was repeated with bells. It is known that he was able to bring some of the eigenfrequencies of the bells of the cathedral at Utrecht into resonance by whistling. One should therefore not be surprised that, as a result of this discovery, Van Eijck was able to accurately formulate objections against the nonharmonic bell of his time. For he could sound each overtone of a bell separately, one by one, for the purpose of comparison of the overtones to acceptable musical intervals.11
Van Eijck's ingenious method made heavy demands on one's musical hearing, therefore his discovery was not applied very much in bell founding. A more appropriate variation had to appear. This variation, first used by the Hemony brothers in the first half of the seventeenth century, was also based on the resonance phenomenon but in the reverse sequence. The Hemonys had a number of sounding rods of iron or brass, which by means of an organ or a harpsichord had been tuned accurately to the desired frequencies of a bell's partials. A correctly tuned bell, when struck, would then bring the rods into resonance. Because of the great intensity of the sounding bell, it was not always easy to tell if the rod did come into resonance. This was later refined by the use of sand; the resonating rod would leave the sand around it lying at the nodes and jumping away from the antinodes. This formed the simplest vibration patterns of Chladni, long before he described them.12
Working with these fascinating resonating rods remained a custom until the nineteenth century. Though this method was correct, the difficulty was that the rods could not be tuned continuously. Thus one had only a series of fixed frequency references. This meant that one had to compare an untuned bell overtone with the rod by listening, a method completely fine for good musical ears, but with the potential for error due to fatigue.
In the nineteenth century an instrument was developed with continuously variable frequency. This was done by fastening weights on the prongs of a tuning fork. By shifting these weights the frequency of the tuning fork could be changed. By calibrating the tuning fork frequency with weight position, one could set any desirable frequency. Also, bell partials could be brought. into resonance by striking the tuning fork and placing its stem on the surface of the bell.
Though this technique was used in many bell foundries, since 1945 an electronic device has come into use that uses an electronic oscillator and transducer. The oscillator frequency is settable to an accuracy of 0.2% or about 3 cents. The coil and driving amplitude can be set to put the bell into continuous resonance at various intensities.
TUNING THE BELL
When Pieter Hemony died in 1680, his niece Anna Margaretha Hemony wrote to a friend that she doubted if her Uncle Pieter had really taught the "real secret" to his successor Mammes Fremy. Almost ten years later the Antwerp bell founder Melchior de Haze sighed unhappily that Pieter probably took the secret with him to the grave. In both cases they were talking about the tuning of bells.
In spite of all the romantic theories, in the present time the tuning technique cannot be called a secret. In the nineteenth century A. B. Simpson, an English cleric, published some interesting data on this. The latest revelation, based on his own investigations, was prepared in 1949 by E. W. Van Heuven of Delft, in his dissertation on "Acoustical Measurements on Church Bells and Carillons." Without any romanticizing elements, it describes the first elements of tuning.
One could define bell tuning as changing a bell's profile by thinning its wall so that the lowest five overtones attain harmonic proportions. It might seem much simpler to correct the bell-wall thickness beforehand in casting, but this is not possible. During forming and pouring there are so many uncalculable factors such as mold shrinkage, that it is practically impossible to give the bell exactly the shape that theory prescribes. It is more practical to cast the bell thicker than necessary, as was done in the beginning of the seventeenth century. The process of tuning would then turn the bell down to the correct thickness.
Although in theory it should be possible to give the cast bell its correct form by measuring the wall thickness in various places and then calculating how much should be turned down, this also is impossible. It has always been the practice to measure the overtone structure during thinning, and use this as a guide to determining which places have to be thinned.
Because of the different vibration pattern for each bell overtone, it is clear that thinning the bell wall at any particular place will not give the same frequency change for all overtones. This means that for each bell overtone one has to know the frequency change as a function of wall thinning along the profile of the bell.
Such functions for tuning are only used for the inside surface of the bell, because the outside of the bell, according to tradition, is provided with ornamentations and inscriptions. One wants to tune a bell by turning down the inside, not the outside, which is reserved for ornamentation.
What is the ideal tone structure? Can this be imitated by other musical instruments or does the bell have its own ideal?
As noted before, no percussion instrument, including the bell, has a harmonic overtone structure "by nature." This means that the eigenfrequencies cannot be expressed as arithmetically simple ratios. This is, as one knows, very different from a string or an organ pipe whose eigenfrequencies can be expressed as 1:2:3:4:5, and so on. However, if we take any bell from the time when little attention was given to the overtone structure, one finds for example lowest eigenfrequencies in the ratios of 1.00: 2.07: 2.24: 3.09: 3.76 or 1.00: 1.78: 2.61: 2.76: 4.41. In contrast with the completely elastic string or vibrating air column, then, is the bell or other percussion instrument where certain provisions have to be made to make this arithmetically complicated series simpler and more acceptable for musical hearing.
A simple comparison between the example above and the harmonic tone series shows that differences appear not only in their anharmonic and harmonic character, but also that the partials for the bell are much more condensed. In the case of the stringed instrument, the fifth partial is five times the fundamental, while for the bell the fifth partial is only about four times the lowest partial. Therefore, it is possible to see that it is almost impossible to transform the overtone series of a bell to that of a string. One should therefore be content with obtaining a harmonic relation of a higher order where only certain ratios are lacking.
This latter idea turns out to be possible. After the introduction of the template in the beginning of the fourteenth century, bell science gradually developed and made it possible in the beginning of the seventeenth century to give the lowest eigenfrequencies of the bell the ratios 5:10:12:15:20. It is interesting that these can also be expressed as 1/12: 1/6: l/5: 1/4: 1/3-a remarkable fact that indicates that the minor third is dominant in the bell's sound.
It is natural to understand that the bell founder, and even more the musician, do not work with frequencies or ratios of frequencies. They prefer to express the frequencies as notes to show directly the musical acceptability of certain bell sounds. In this case the tone series can be expressed as c-cl-eb1-gl-C2, (C3-C4-E4b-G4-C5) in which the hum tone is c in this example. In bell founding these partials have acquired their own names of hum tone, prime, tierce, quint, and nominal.
One could remark that this harmonic series for the bell is realized only for the lowest five eigenfrequencies, while for the string or organ pipe the harmonic series is maintained over a considerable greater number of overtones. This is correct, but in connection with other bell-sound factors, it is not as important as it seems. In the first place, higher overtones have a lesser volume and are of shorter duration. Furthermore, a large number of higher partials have a node at the place where the ball is struck; these overtones will be considerably weakened. One can remark that in the development of the bell, the aim has been to localize the striking point, or conversely, to pay attention to those partials that are the loudest. Finally, one can say that those higher partials are heard best which have fairly exact harmonic values and, as will be shown, are strongly anchored in the structure of the lowest five partials. Indeed, with very fine tuning, the higher strong partials join themselves to some degree into the harmonic scheme.
The bell founder will first aim at realizing the first five partials.
Let us assume that the profile is approximately correct and that the wall
thickness is a little greater than necessary (about 1/2 mm too thick).
Then he tries to reach his bell ideal by tuning.
| bes | bes1 | des2 | f2 | bes2 | |
| ongestemd |
44
|
48
|
34
|
56
|
26
|
| c - t |
24
|
40
|
20
|
32
|
14
|
| d - t |
6
|
34
|
10
|
13
|
6
|
| d - f |
4
|
29
|
8
|
10
|
2
|
| e - g |
0
|
27
|
6
|
8
|
0
|
| q - s |
0
|
11
|
5
|
4
|
0
|
| s - t |
0
|
0
|
4
|
1
|
0
|
Table 1. The tuning process for a bell bes1 (B4b), diameter 860mm.
Note: The first line gives the lowest five partials, the second their deviation in cents from the correct tuning. In the next lines the first column shows in which sectors bronze has been removed, while the next columns give the result. Before tuning, this bell weighed 427 kg, after tuning 418 kg.
Take for example the tone structure of a freshly cast bell given in Table 1. If we assume that the bell in this example must be tuned to a standard pitch, then each of the partials must be tuned down. If local wall thinnings were to affect each partial equally, then it would be impossible to tune the bell. To tune, one has to have accurate information relating how metal removal at every level affects the pitch of each partial to be tuned. The production of such tuning graphs is experimentally not very difficult. The inside of the bell is divided into a number of ring-shaped sectors of equal width. As a unit of width one can take 1/25 of the diameter of the bell (Fig. 1). Next, in every sector starting with "a", a measured amount of brass is turned down and the pitch shift for each partial is recorded. One moves on to sector "b" In this way Figure 2 has been obtained. The sectors are graphed horizontally while the pitch changes are noted vertically.
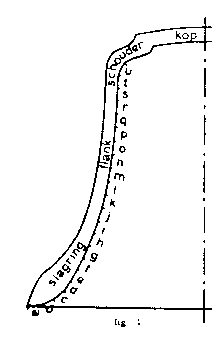 |
Figure 1. To determine the tuning curves the inside of the bell is divided into horizontal sectors of width 1/2s of the bell diameter. Then for each partial the tone change is measured for removing metal from each sector. The results of the measurements are graphed in Figure 2. |
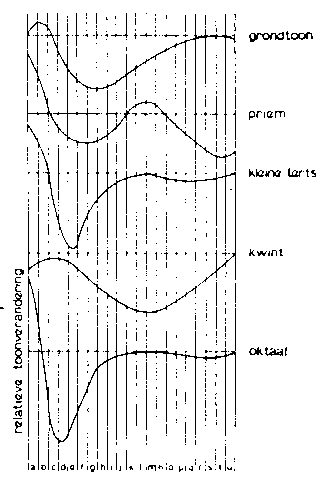 |
Figure2. The relative pitch deviation of the lowest five partials as a function of the sector when a certain amount of bronze is removed. |
With the help of these graphs the bell founder will easily tune an untuned bell, see for example, Table 1. In the first column one finds the sectors in which bronze has been turned off. The following columns show the results.
One can see from this table that tuning takes place step by step. The reason is that the smallest amount of excess removal of bronze would irreparably change the bell. Moreover, elaborate calculations would be necessary to determine a priori with the tuning curves the amount of bronze needed to be removed. Therefore, the bell tuner always works with relative values as used in Figure 2.
It should be noted that, although these tuning graphs are very useful, there are limitations. For example, if the fourth partial were too low, this could not be corrected by means of wall thinning. The tuning curve shows that in each sector the pitch of the fourth partial will fall if metal is removed. Does this mean that the other partials can be tuned up? Theoretically this seems possible. In practice there are considerable limitations. The tuning curves show that the sectors for pitch raising are very few. If one wanted to raise the pitch of an overtone a large amount, a large amount of metal would have to be removed. In principle this is possible but the profile would be changed by excessive local removal. One must consider that a smooth profile strongly affects the tone color. Local wall thinning can be used to change overtone tuning over a wide range, but there are other reasons why this is not advisable. One can generalize that extreme local metal removal introduces discontinuities that are disasterous. For example, if one would like to tune the fifth partial by removing much metal in sector d, one would get a groove that would hurt the sound of the bell.
Tuning a bell is not simply a question of setting a number of characteristic frequencies. One always has to rely on hearing for the tone color of the bell, or apply certain rules of experience. All of this shows that designing a bell profile is certainly not a random matter, and that all imperfections cannot be corrected during tuning.
The designing of a bell is in fact a rough pretuning. For this the tuning curves for the inside of the bell are not sufficient. Besides having tuning curves for the outside of the bell, one also has to have other rules which relate tone structure to bell profile-the relationship between the eigenfrequencies and the height of the bell, for example. One can ask how appropriate the tuning curves are for various profiles. Of course this question should have been asked much earlier. If one starts in sector "a" and shaves off metal to sector "u", he ends up with a different bell. Experiments show, however, that even if one removed metal in the other direction the same results are obtained. This independent character of tuning curves is also valid for not very different bell profiles. In these cases, only minor changes in the tuning curves occur. Therefore, the curves are a very reliable tool in the design of a bell.
A last and very important question in connection with bell tuning is what degree of tone purity should be aimed for? Of course the criterion here can only be musical, although simultaneously a very complicated problem is introduced.
Considering a single bell, not heard in consonance with others, one has the requirement that the intervals to be realized between the lowest five partials should be perfect, and heard as such. Experience has shown that this requirement is only satisfied when the eigenfrequencies of the bell are tuned to an accuracy of 0.2% or 3 cents. Nevertheless, it is dangerous to apply such a rule without further thought. In low bells this can lead to disturbing beats between the partials themselves. For example, if the hum tone of a bell forms a subjective harmonic an octave higher and the hum tone is 3 cents low, then the subjective harmonic will give beats with the prime. This shows that in the final analysis musical hearing is the ultimate criterion.
When several bells sound together, the same rules are valid; however, the danger of beats is much larger and therefore more attention has to be paid to this aspect. For example, if a bell with hum tone c1 (C4) whose tierce is es2 (E5b) were to sound with a bell whose prime was es2 (E5b), then very disagreeable beats will occur if both partials do not have exactly the same frequency. One needs to tune a set of bells externally as well as each individual bell internally. This makes for a complicated tuning process. Each amount of bronze turned down from a bell should be extremely well considered. A bell thinned by too much, however little, cannot be restored to its original condition.
Curiously enough, in this process of beatless tuning, the technique of using accurate measurement apparatus is insufficient. In the final fine tuning one is entirely dependent on the musical ear the same ear that in carillon playing hears beats between bells immediately and experiences them as disturbing the harmonic consonance.
I should mention that the picture given so far of tuning carillon bells reflects the developments of the last few years. Before this, one was content to tune bells within 3 cents and not to care too much about beats that would occur. Even the famous Hemony bell founders of the seventeenth century, who left numerous excellent carillons in The Netherlands, limited themselves to this accuracy of 3 cents,13 an amazing accomplishment for the bell foundry art of that time. In spite of this, one must state that considerable improvement has now been made in tuning techniques so that beat-free carillon tuning has now become possible. This is especially important for the place of bells in the development of contemporary music.
PARTIAL GROUPS IN THE BELL SOUND14
In the foregoing we concerned ourselves exclusively with the lowest five partials of a bell and spoke only secondarily about higher partials. This does not mean, however, that higher partials are musically of less value or that their spectral position is arbitrary. On the other hand, not all high partials have the same significance. The criterion here is, without any doubt, their strength during the bell strike. This would mean that the overtone strength for every bell would have to be measured to determine which higher partials are really important. Unfortunately, determining such a spectrum during normal bell founding is nearly impossible. Of course, there are analysers that will isolate certain bell frequencies, making it possible to measure partials separately. However, these analysers usually have too low a selectivity to measure strength of partials one by one unless time-consuming measurements are made. If one considers that many higher partials have frequencies less than 10% of each other, then this difficulty will be very clear. Fixing the frequency spectrum of a bell generally must be done in a laboratory, and this is a considerable limitation. One has to look for other methods for finding the strengths of bell overtones.
It is clear that one has to look for the characteristic function of the overtone in question, that is the function in which the radial wall amplitudes for each point of the bell surface are given. It is the radial wall amplitudes that determine the total volume of an overtone. Determining such functions is done in the following way.
After the bell has been brought into steady-state vibration for a certain overtone by means of an electrodynamic excitator, one uses a recorder employing an exciter used inversely to convert the mechanical bell vibrations into an A.C. voltage. Because the voltage is proportional to velocity, one has to use an electronic integrator to convert the velocity signal to a displacement signal. If, then, the recorder has scanned the whole bell surface one would have enough information to put together the necessary characteristic function. Because of the particular symmetry of the bell one can best split these measurements into circular and meridional sections. Of course the meridian measurements are the most interesting. In Figure 4 the characteristic functions for a large number of overtones of an arbitrary bell are given for an outside meridian. The bell had a diameter of 97 cm and weighed 567 kg. Its strike tone was gis1 (G4#). The measured characteristic frequencies for this bell are given in Table 2 with the traditional partial names.
We should give an elaborate discussion of errors. However, only some summary observations will be made. When one examines other bells for comparison there are small deviations in the characteristic functions, but the form of the graph is nevertheless the same. This means the above graphs can be applied to any bell provided it has normal proportions. One could aim at measuring absolute amplitudes.
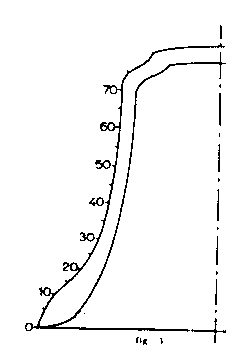 |
Figure 3. A bell, tone gis1(G4#); diameter 97 cm, weight 567 kg, on which the radial wall amplitudes for Figure 4 have been determined. The strike point for this bell lies on the outside of the bell 10 cm above the lip measured along the bell surface. |
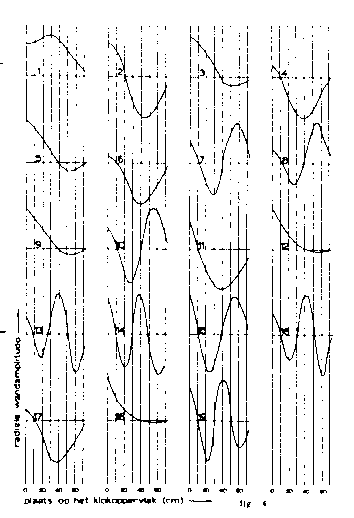 |
Figure 4. The radial wall amplitudes in a relative measurement, measured on the outside surface of the bell along a meridian of the bell in Figure3. Measurements for each partial of Table 2 are given. The strike point is about 10 cm from the lip. |
This does not make sense, however, for the graphs above were created by electrodynamic excitation, not by a clapper. Even if one could consider tone formation by the clapper one would have to also consider the hardness of the clapper. A soft clapper would diminish upper partial strength, as would a relatively heavy clapper. The mean amplitude of each function is variable, dependent upon the manner in which the bell is struck. In view of the way in which these characteristic functions have been obtained, it does not make sense to measure absolute amplitude. Therefore, all the graphs are normalized to have the same peak amplitude.
In spite of these limitations one can say something in a relative sense about the volume to be expected from each partial. If a bell is struck on one of the nodal lines for a certain mode, one can certainly expect a low amplitude for the corresponding partial. Striking at an antinode would emphasize the partial.
 |
|
Table 2. Frequency analysis of a bell, G1#, diameter 970 mm, weight 567 kg. Note: The second column gives the names customary in bell founding for the most important partials. The fifth column gives the number of nodal meridians; the sixth column, the eigenfunction group derived in Figure 5 from Figure 4. The seventh column gives the physical name of the partials based on their eigenfunction group and number of nodal meridians. The last column gives the relative musical position of most of the partials when the hum tone is defined as C. |
Considering that the striking point for a bell is nearly fixed, then one can quite reliably say that partials with nodal circles near the strike point would be heard weakly. Partials with nodal circles far from the striking point will be heard loudly. In this way one can observe that the hum tone, prime, tierce, nominal, twelfth, double-octave, etc. will be dominant in the spectrum. Interesting is that this sequence gives a relative tone scale c - c1 - es1 - c2 - g2 - c3 (C3 - C4 - E4b - C5 - G5 - C6), which is very acceptable. Conversely the weaker partials give a much less harmonic series g1 - e2 - f2 (double) - a2 - b2 (G4 - E5 - F5 - A5 - B5), and so forth.
All of the amplitude functions given are measured over meridians of the bell surface. To complete the picture of the vibrating bell one should also investigate wall movements along circular lines around the bell. Because of the circular symmetry of the bell, these will be much simpler. One can expect a strong analogy with a vibrating ring.15 Each overtone can be characterized by a number of nodes equally spaced around the circumference of the bell in which the wall movement between nodes can be approximated by a sine function. In Table 2, column 4, the number of nodal lines vertically down the surface of the bell are given for each overtone. We have deviated from the usual notation in bell literature. Usually one counts the number of nodes found when going completely around the bell once. However, if one correctly considers the bell as a bent plate, we can follow the notation that is customary in scientific literature; this is half of the bell founder's count.
The nodes that one counts going around an arbitrary parallel will be seen as radial lines. Observing the bell from above one sees the radial lines as half the number of lines simply crossing at the crown of the bell. This halved count is indicated in column "s" of Table 2 for every partial; for example, the hum tone having four radial nodes is seen as having only two intersecting nodal lines when viewed from above.
Since we are dealing with a circularly symmetric body, the positions of the meridional nodes are determined by the strike point of the bell. For the hum tone and the prime the meridional nodes will be 450 and 1350 both to the left and right of the strike point. In this consideration one assumes an antinode for all partials is formed at the strike point.
By means of the meridional and circular nodal lines the modes of vibration of a bell can be completely described. The next step is to order and interpret these eigenfunctions. The number of circular nodes, as described before, serve as one sort of classification. Certain patterns return time and again. Figure 5 collects the averages of the characteristic amplitude functions divided into the classes of modes. Every basic pattern, or class, is indicated by a Roman numeral.
Aside from the fundamental and the prime, it is possible to classify partials into groups which have the same circular node pattern. The averages of the first four classes of partials are taken from Figure 4 and given above in Figure 5. The Roman numeral groupings in Table 2 correspond with the Roman numerals above.
In view of the fact that one particular circular node can be contained in several different partials, a basis for grouping the partials is formed. Partials with a particular nodal pattern can be grouped together. From Table 2 and Figures 4 and 5 one can distinguish the following groups:
Group I. Partials from this group are characterized by a large amplitude
at the sound bow and a nodal circle in the waist of the bell. The lowest
partial with s=2 is lacking since neither the hum tone or the prime have
a nodal pattern corresponding to this group.
Group II. Partials in this group contain a nodal circle in the sound bow
and an antinode in the waist of the bell. Here again, for reasons mentioned
earlier, the nodal pattern with s=2 is lacking, although the prime is
a close approximation to the s=2 member.
Group III. The partials in this group contain one more nodal circle than
the foregoing groups. (2 nodal circles)
Group IV Three nodal circles characterize members of this group. The amplitude
function over the surface of the bell is described approximately by a
sinusoidal curve.
Group V, and higher contains each time one more nodal circle than the
preceding group. The amplitude functions tend more and more towards a
pure sinusoidal curve.
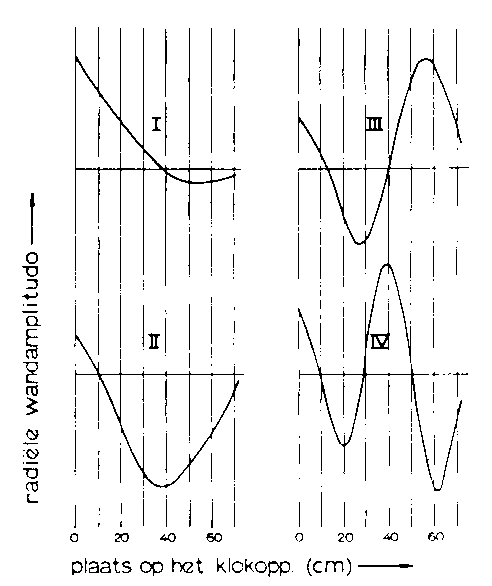 |
Figure 5. Aside from the fundamental and the prime, it is possible to classify partials into groups which have the same circular mode pattern. The averages of the first four classes of partials are taken from Figure 4 and given above in Figure 5. The Roman numeral groupings in Table 2 correspond with the Roman numerals above.
|
The lowest two partials of the bell, the hum tone and the prime, curiously seem to stand outside of the group classifications given. Nevertheless, one can show that the hum tone is the lowest member of Group I and the prime the lowest of Group II. This can be shown by constructing an experimental bell profile which is purely conical. If one investigates the modes of vibration on such a conical bell, one notices the following interesting changes. It appears that the nodal circle for Group I is shifted to the crown of the bell. This means that the modes of vibration for Group I are practically identical with the mode for the hum tone, so it seems justified to consider the hum tone as the lowest member of Group I. Something similar is valid for the partials of the second group. The nodal circle for Group II in a conical bell lies near the position of the nodal circle for the prime in the normal profile bell. For this reason the prime can be considered the lowest member of Group II.
Starting with the foregoing considerations, it should not be difficult to represent the partial groups graphically. This has been done in Figure6 for the bell of Table2. The number of nodal meridians is given horizontally, the partial frequencies, vertically. The connecting curves represent the progression of members of one group.
Any partial can now be unambiguously identified by its group and the number of vertical meridional nodes. Is it easy to indicate this in a partial's name? This seems advantageous, since in the past partials have been named by the relative musical position, such as the prime.16 Such labeling cannot be unambiguous since the musical interval position of a partial is highly dependent on the bell profile. It is much better to consider the physical aspects of each overtone in giving a name, aspects which are less dependent on bell shape. In this way partials may be named by two members. The first is a Roman numeral indicating the group and the second number indicates the number of nodal meridians, s. Thus the hum tone becomes I-2, the prime II-2, and so forth (see Table 2).
 |
Figure 6. Graphic representation of the group classifications for the bell in Table 2.
|
The starting point of our considerations was to understand simply which partials could be considered musically important. After measuring the eigenfunctions for one bell, one asks if it is necessary to repeat the measurements for each bell. Fortunately, it is not necessary; every bell has the aforementioned modes of vibration. Each mode is characterized by its physical name which gives the circular node group and the number of nodal meridians. One only needs to look for these characteristic modes; the following procedure is used. By means of the electrodynamic excitator described earlier, the bell is brought into steady-state vibration for the partial to be investigated. The bell surface is scanned with a pickup transducer; the voltage induced on the pickup will show where the nodes occur on the bell. Another variant consists of carefully going over the bell surface with a stethoscope. For tones not too high in pitch the minima can be observed by hearing. The final method, which is only suitable for finding nodal circles, makes use of the fact that a partial cannot be excited by striking on one of its nodal circles. In Table 3 results are given for a bell with strike tone g#1, diameter 974 mm, and weight 428 kg. In Figure 7 the group classifications are represented. One can easily see that this graph has great similarities to that of Figure 6. This indicates that the group classification graphs for all approximately tuned bells will give the same results.
 |
|
Table 3. Frequency analysis of a bell gis1 (G4#), diameter 924mm, weight 428 kg. Note: the partial VI-4 was not found. For explanation, see Table 2. |
 |
|
Figure 7. Graphic representation of the group classifications for the bell in Table 3.
|
Can one assume from the examples that a bell is completely described by its frequency structure? This is practically true, but on a theoretical level the description needs to be expanded further.
The eigenfunctions considered so far are all produced by vibrations of the flexural type. This can be made very plausible if one keeps in mind the analogy between a horizontal bell section and a vibrating ring. The theory of flexural vibrations is used when realizing that in the execution of wall movements, one can locate a surface that neither expands nor contracts. That is, a surface which only makes inflections along which no normal or tangential forces appear. Usually this surface is considered to be the midplane of the wall. The radial wall amplitudes would then be perpendicular to this cylindrical surface. In order to imagine such a non-expanding or contracting cylinder there would have to be at least four motionless points on the circumference, that is, at least four radial nodes. The number "s" should therefore be at least two. For vibration nodes where s=0 or 1, there cannot be such a neutral surface. In this case one has to speak of stretch vibrations. Do these stretch vibrations occur in a bell?
From the nature of these modes one would expect that they would naturally have a high frequency. Indeed, this is confirmed experimentally. The first stretch type partial in a normal bell occurs at a frequency between that of partials I-4 and II-4. All others have a higher position yet in the frequency spectrum.
In spite of these circumstances that make the stretch vibrations seem less important, one can still ask why they have not been included in the foregoing considerations. It turns out that all the stretch vibrations have an antinode in the crown of the bell, from which the bell is normally hung fixed. Thus, these stretch modes will barely be heard, if at all. Even if the antinode in the crown of the bell is allowed to develop completely, the amplitude of vibrations in the side and sound bow of the bell remain small. For this reason it makes no sense to completely describe the stretch vibrations. Only in small bells with a relatively thick wall can they be of any significance at all.
Apart from the musical consequences, which we will deal with later, the system of group classification offers a means of profile investigation. In the past, a bell could not be physically related to other vibrating bodies such as the gong. Now, however, on the basis of the eigenfunctions, this is possible. For if the bell is gradually changed through several intermediate shapes, one can always identify in the new shape those partials that correspond to partials of the original bell shape, regardless of how much the partials have shifted or changed position in the sound spectrum. It is even possible to bypass these intermediate shapes and by means of eigenfunctions alone indicate partials that relate to bell partials. In the gong, for example, a study by Grutzmacher and Wesselhoftl7 shows that partial groups in a bell compare to partial groups in a gong, where similarly the first group dominates, while other groups have a secondary function. Such a connection with the bell would be impossible to make on the basis of the sound spectrum alone.
MUSICAL CONSEQUENCES
By means of group classification it should not be difficult to predict the relative spectral distribution of the various eigenfrequencies of a bell.
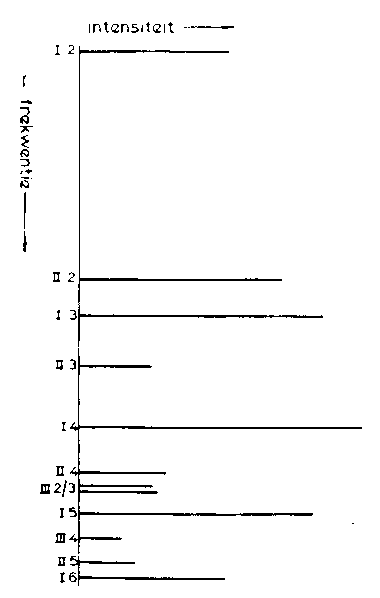
We observed earlier that those partials having no nodal circles at the sound bow especially dominate the sound spectrum of a bell. This includes the partials of group I and partial II-2, the prime, as well. In musical terms, this is approximately the series c - c1 - es1 - c2 - g2 - c3 - f3 - a3 - c4 (C3 - C4 - E4b - C5 - G5 - C6 - F6 - A6 - C7). In Figure 8 the average sound spectrum of ten bells is given, and it appears that these tones clearly are stronger than others. The essentially nonharmonic spectrum of the bell has been made quite acceptable in this way, for it is the dominant overtones that reinforce the tuned pitch of the bell. Nevertheless, some questions remain that merit consideration. One can ask why only the lowest five partials are tuned when our consideration above involves higher partials as well. One assumes then that tuning higher partials might be possible. In practice however this is not feasible. It has been found that partials with nearly identical eigenfunctions have very similar tuning curves as well. One can observe this for the partials I-3 and I-4, for example (see Fig. 2). This implies that one can rarely tune separate partials within the same group. We illustrate this with an example. It is clear from Tables 2 and 3 that the pitch of partial I-6 is rather sharp, a common occurrence in most bells. Naturally it would be attractive to make this partial I-6 be a perfect octave above partial I-4. The tuning process for this uses practical the same tuning curves for the partials I-4 and I-6. This means that if the pitch of one of the partials is changed by some amount the other partial will change practically to the same degree. To tune these partials separately, then, one would have to make use of detailed differences between the tuning curves of the two partials, and the bell profile would have to undergo much localized thinning. One would introduce in the profile a discontinuity that would have undesirable consequences for the timbre of the bell. Other partials would take on quite arbitrary positions in the sound spectrum of the bell, so that what one gains with one partial, one loses with the others.
In this way we have indicated the possibilities for tuning with greater accuracy. If one assumes that partials with the same eigenfunctions have practically the same tuning functions, then large tuning changes are possible only for the hum tone I-2, the prime II-2, and among different groups. Partials within one group allow only small independent corrections. One should realize that this last statement is quite significant for the musical aspects of the bell!
Finally, one has to consider that tuning bell partials upwards is generally not advisable. All of these factors limit tuning possibilities considerably, and one should weigh these factors when designing a bell. Does this mean that one is totally bound to the tone structure of an individual group and that relations within a group are practically independent of bell profile? Yes, up to a certain point. The design of a bell allows great possibilities, but one has to avoid discontinuities in designing a bell profile. Consideration must be given to more than just wall thickness. One can vary the slope of the bell profile, the height or diameter of the bell, and so forth. This means that the designer can do something about internal relationships within a group. But one cannot expect too much, for experience shows us that to conserve the harmonic structure of the lowest partials, a variation of 4% in frequency is maximum. As a consequence, the major third bell, with partial I-3 a major third above the prime, has not yet been realized, in spite of the claims of certain bell founders. Also it is not possible to make the interval between I-3 and I-4 a perfect octave. Even in the Chinese gong with a design much different than our normal bell, partial I-3 is 10% from the octave frequency of I-4.18
Although the strong structure within a group can have some bad consequences musically, this is an advantage in other ways during tuning. To take a very crude attitude towards the tuning process, one might consider it sufficient to tune only the important lower harmonic partials that have different eigenfunctions and therefore different tuning curves. This would be the sequence: hum tone I-2, prime II-2, quint II-3 and octave I-4. If then, by the design of the bell, sufficiently pure relationships within a group were chosen nothing essential will be changed if tuning is done within reasonable bounds. This means that the tierce I-3 would have a reasonable purity, as would the twelfth I-5 and double octave I-6.
 |
|
Figure 8. Average intensity distribution of the partials of 10 normal bells struck in the customary way. It is clear that the first group of partials occupies a dominant position. |
The bell founder however, cannot be satisfied with such a crude approach to tuning. He will at least try to use the detailed differences in the tuning curves of I-3 and I-4 to fix the partial I-3 as harmonically pure as possible, for the partial I-3 occupies a very dominant position in the spectrum of a bell (Fig. 8). But with this the possibilities for fine tuning are practically exhausted. The bellfounder will have to be content with fixing only reasonably well the 12th I-5 and the double octave I-6, without being able to change them much during tuning. This is also true for the partial II-4. The ability to correctly place partials is finally exhausted when considering group III with its curious lowest partials of flatted tenths.
Summarizing, one can state that the final result of designing and tuning a bell can at most assure that the partials I-2, II-2, I-3, II-3 and I-4 are highly pure, that is, within 0.2% of the correct frequency. The higher partials will relate to the lowest five partials, depending on their particular eigenfunctions, with a purity of 0.5 to 5% of the desired frequency. So bell tuning is a compromise, particularly involving the lone purity of the higher strong partials.
We have seen that the group classification of partials is of great significance to the tuning and designing of a bell, as well as many other aspects of a bell's sound. Repeatedly in scientific bell literature we find a listing of the eigenfrequencies as if it would give us complete insight into the sound of a bell. One even goes so far as to draw extreme conclusions from such listings of eigenfrequencies.19 Such a procedure however is not at all possible. For how can one locate the double octave in such a list?
Tables 2 and 3 show that near the partial I-6 there occur several partials, for example those from group IV. Based on the frequency analysis of several bells, it is not at all impossible for a tone of group IV to form an exact octave with I-4, while I-6 remains too high. Can one consider this tone of group IV as a double octave? Certainly not in general, the impression of a musician relates to the strongly audible partials. It therefore makes no sense to let a weak but pure partial prevail over a strong but less pure partial because of its more precise harmonic position. The conclusion is then that even if the partial I-6 has deviations in tonal purity, the ear will still consider this tone as the double octave. This means that when one is given the eigenfrequencies, one also has to be informed of the corresponding eigenfunctions. This information is easily stated with our nomenclature, in which the number of nodal circles and nodal meridians is given. This difficulty not only occurs with the double octave, but also with other partials. Among others this is true for the flatted double tenth I-7, a tone that can be very disturbing, especially in heavier bells. Another phenomenon that can be illuminated by group classification is one many musicians have correctly observed: that the bell, with its conspicuous minor third, gives rise to confusion in carillon playing when a melody is in a major key. Correctly then, the musicians state that the minor third should be as weak as possible. Physically this means that by suitable bell model choice the nodal circle for the third has to be lowered as much as possible toward the sound bow.
Apart from the question of whether this is possible or not, one has to consider seriously that the nodal circles of the other partials of group I would be shifted down by approximately the same degree. However, it is exactly in this group that the bell sound finds a strong basis for unambiguous tonal height. Thus, a weaker third opposes the production of a strong tonal height sensation for the bell; it is clear in such a choice what we would prefer. All this and more demonstrates that group classification is an important aspect of bell science. One can return to group classification time and again if one wants to understand the observed phenomena. This systematic ordering on the basis of the most fundamental properties of partials is also important in the decay rates of the partials in the production of difference tones, and in the problem of the strike tone about which Prof. Schouten reports more extensively [Editor's Note: See Paper 15.]
The same group classification will also form a foundation for the investigation of timbre, a subject for which a coherent physical picture is totally lacking. Certainly several have been given, but the problem is so complicated that research on this very important aspect of bells is only beginning. Many factors are involved, because apart from the profile of the bell, the upper structure and the decay times play an essential role. Also important are the bronze used to cast the bell, the quality of the cast work, the manner in which the bell is struck, the place where the bell is hung, the audition location, and especially the interpretation that the listener gives to the physically measurable facts. Here we return to our point of departure, for however fascinating a bell is as a physical object, finally it is only the listener that can give value to the measurable aspects.
REFERENCES
1) For an extensive orientation in this subject, see "Bells and Bell
Founders. Contributions to Campanology," a collection of historical narratives
of the Historical Commission of the Dutch Carillon Organization (Culemborg,
1963). A list of important publications on this subject is also included.
2) Winfred Ellerhorst: Handbuch der Glockenkunde (Weingarten 1957), blz.
10; Andreas Weissenback und Josef Pfundner: Tonendes Erz (Graz-Koln, 1961),
p. 1.
3) Curt Sachs: the History of Musical Instruments (New York, 1940), p.
164 ff.
4) A. Wood: de Natuurkunde der Muziek (Amsterdam' 1949), p. 183 ff.
5) J. Smits van Waesberghe: Cymbala (Rome 1951).
6) A. Lehr: Middeleeuwse Klokkengietkunst (in Klokken en Klokkengieters,
1.c.), p. 126 ff.
7) Rayleigh: the Theory of Sound, paragraph 235b ff.
8) A. Lehr: Middeleeuwse Klokkengietkunst, 1.c., p. 23 ff.
9) A. Lehr: de Klokkengieters Francois en Pieter Hemony (Asten, 1959).
10) Klokken en Klokkengieters, 1.c., p. 279
11) de Klokkengieters F. en P. Hemony, 1.c., p. 26 ff.
12) An extensive article on this subject by the Author has appeared in
Janus, international review of the history of science, medicine, pharmacy,
and technology.
13) A. Lehr: the system of the Hemony-carillons tuning (Acustica, vol.
1, 1951, p. 101-104); A. Lehr: Historische en muzikale aspekten van Hemony-beiaarden
(Amsterdam, 1960), p. 38 ff.
14) This investigation was carried out during 1953-55.
15) Rayleigh, 1.c., paragraph 232 ff.
16) Such a wrong assumption appeared, for example, in "Proposed American
Standard Procedures for the Testing of Bells and Bell Instruments" (American
National Standards Association May 15, 1956); also by Josef Pfundner "Uber
den Schlagton der Glocken," Acustica 12, 153-57 (1962).
17) M.Grutzmacher und E. Wesselhoft: Uber den Klang eines Chinesischen
Gonges (Acustica, 9, 1959, pp. 221-223).
18) Grutzmacher en Wesseihoft, 1.c.
19) Pfundner, 1.c.; E. Thienhaus, Akoestische Beihefte 1952, p. 251 ff.
Last updated January 22, 2001. Borrowed from siite created by Bill Hibbert, Great Bookham, Surrey